【算法面试】leetcode最常见的150道前端面试题 --- 简单题下（44题）

本文题目选自 LeetCode 精选 TOP 面试题，这些题在自己和同事亲身经历中，确实遇到的几率在百分之80%以上（成都和北京的前端岗位）。

上版本部分请参考# 简单题上

二叉树（DFS）

二叉树前中后遍历套路详解

前序遍历题目如下：

root节点是A节点（下图的A节点），然后让你按照下图数字的顺序依次打印出节点。

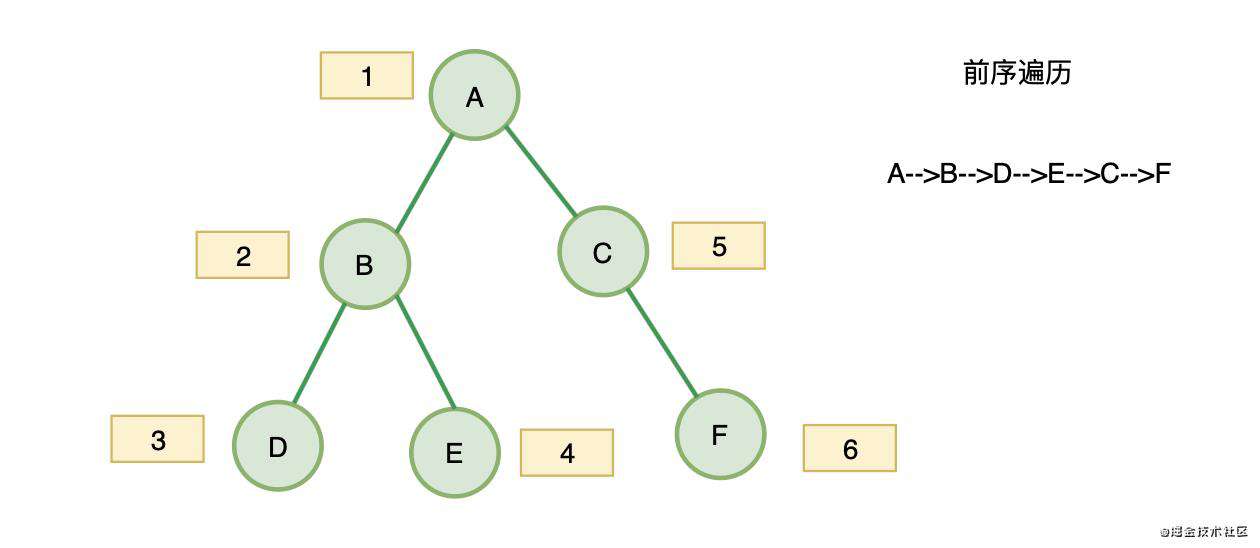
我们可以看到这其中的规律，就是深度优先遍历，先遍历左子树，再遍历右子树，这里我们不用递归，因为一些大厂严格要求二叉树遍历不用递归，递归太简单了。

重点思路就是：深度优先遍历，先遍历左子树，再遍历右子树，

所以，我们需要一套如何遍历一颗二叉树，并且是先左子树，再右子树的通用模板，如下

var Traversal = function(root) {
    const stack = [];
    while (root || stack.length){
      while(root){
        stack.push(root);
        root = root.left;
      }
      root = stack.pop();
      root = root.right;
    }
    return res;
};

我们结合图片发现这个遍历产生的整体压栈的顺序是

• A、B、D入栈，
• D出栈
• B出栈
• E入栈
• E出栈
• A出栈
• C入栈
• C出栈
• F入栈
• F出栈

我们把上面入栈的元素按顺序排列一下就是，A、B、D、E、C、F，而这就是前序遍历的顺序！解答完毕！

是不是很有意思，下面的中序遍历，我们看看出栈顺序是不是中序遍历的要求：D、B、E、A、C、F（这就是中序宾利的要求，好了，两个题解决）

放具体前序遍历代码：

var preorderTraversal = function(root) {
    // 初始化数据
    const res =[];
    const stack = [];
    while (root || stack.length){
      while(root){
        res.push(root.val);
        stack.push(root);
        root = root.left;
      }
      root = stack.pop();
      root = root.right;
    }
    return res;
};

中序遍历是一个意思，在前序遍历的基础上改造一下

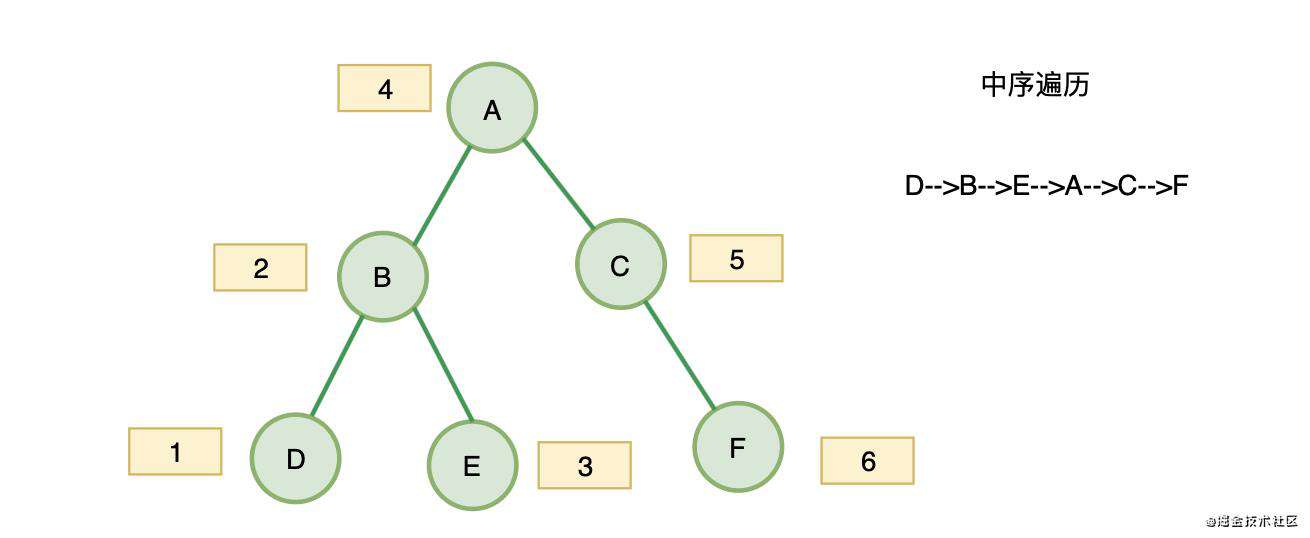
var preorderTraversal = function(root) {
    // 初始化数据
    const res =[];
    const stack = [];
    while (root || stack.length){
      while(root){
        stack.push(root);
        root = root.left;
      }
      root = stack.pop();
      res.push(root.val);
      root = root.right;
    }
    return res;
};

后序遍历有点不太一样，但是套路是一样的，我们需要先遍历右子树，再遍历左子树，反着来，就可以了，代码如下：

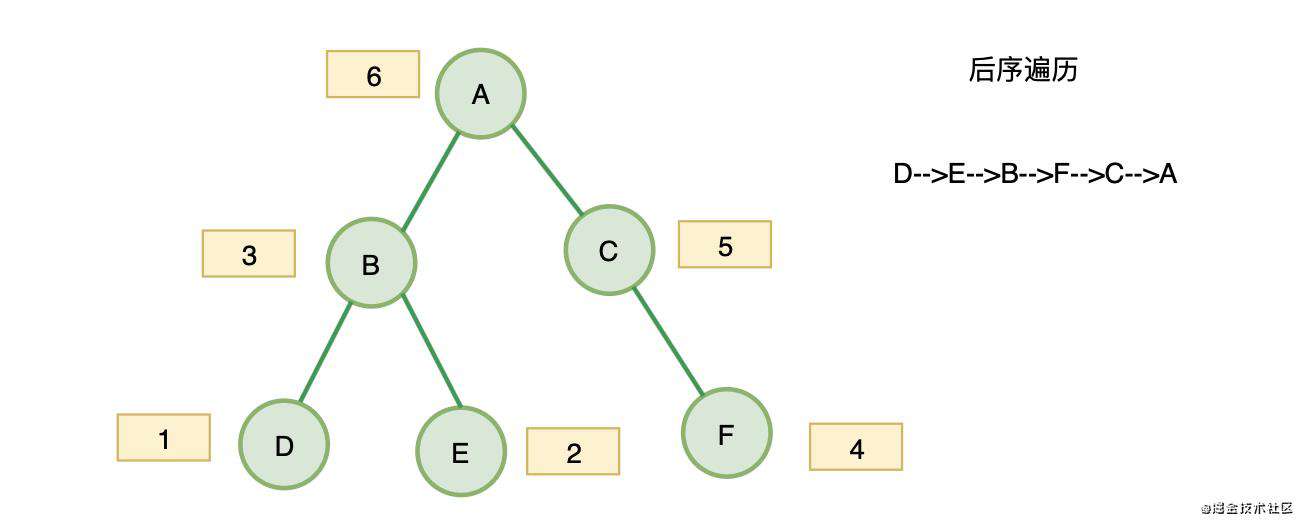
var postorderTraversal = function(root) {
  // 初始化数据
    const res =[];
    const stack = [];
    while (root || stack.length){
      while(root){
        stack.push(root);
        res.unshift(root.val);
        root = root.right;
      }
      root = stack.pop();
      root = root.left;
    }
    return res;
};

对称二叉树

这个题简而言之就是判断一个二叉树是对称的，比如说：

二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

思路：

递归解决：

• 判断两个指针当前节点值是否相等
• 判断 A 的右子树与 B 的左子树是否对称
• 判断 A 的左子树与 B 的右子树是否对称

function isSame(leftNode, rightNode){
    if(leftNode === null && rightNode === null) return true;
    if(leftNode === null || rightNode === null) return false;
    return leftNode.val === rightNode.val && isSame(leftNode.left, rightNode.right) && isSame(leftNode.right, rightNode.left)
}
var isSymmetric = function(root) {
    if(!root) return root;
    return isSame(root.left, root.right);
};

二叉树的最大深度

这个题在面试滴滴的时候遇到过，主要是掌握二叉树遍历的套路

• 只要遍历到这个节点既没有左子树，又没有右子树的时候
• 说明就到底部了，这个时候如果之前记录了深度，就可以比较是否比之前记录的深度大，大就更新深度
• 然后以此类推，一直比较到深度最大的

var maxDepth = function(root) {
    if(!root) return root;
    let ret = 1;
    function dfs(root, depth){
        if(!root.left && !root.right) ret = Math.max(ret, depth);
        if(root.left) dfs(root.left, depth+1);
        if(root.right) dfs(root.right, depth+1);
    }
    dfs(root, ret);
    return ret
};

将有序数组转化为二叉搜索树

我们先看题：

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

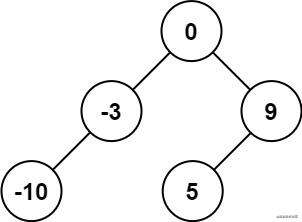
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

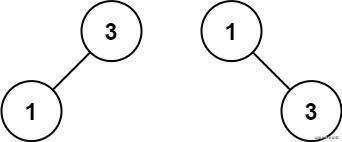
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
 

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列

思路：

• 构建一颗树包括：构建root、构建 root.left 和 root.right
• 题目要求"高度平衡" — 构建 root 时候，选择数组的中间元素作为 root 节点值，即可保持平衡。
• 递归函数可以传递数组，也可以传递指针，选择传递指针的时候： l r 分别代表参与构建BST的数组的首尾索引。

var sortedArrayToBST = function(nums) {
    return toBST(nums, 0, nums.length - 1)
};
const toBST = function(nums, l, r){
    if( l > r){
        return null;
    }
    const mid = l + r >> 1;
    const root = new TreeNode(nums[mid]);
    root.left = toBST(nums, l, mid - 1);
    root.right = toBST(nums, mid + 1, r);

    return root;
}

栈

栈是一种先进先出的数据结构，所以涉及到你需要先进先出这个想法后，就可以使用栈。

其次我觉得栈跟递归很相似，递归是不是先压栈，然后先进来的先出去，就跟函数调用栈一样。

20. 有效的括号

这是一道很典型的用栈解决的问题， 给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。  

示例 1：

输入：s = "()"
输出：true
示例 2：

输入：s = "()[]{}"
输出：true
示例 3：

输入：s = "(]"
输出：false
示例 4：

输入：s = "([)]"
输出：false

思路： 这道题有一规律：

1. 右括号前面，必须是相对应的左括号，才能抵消！
2. 右括号前面，不是对应的左括号，那么该字符串，一定不是有效的括号！

也就是说左括号我们直接放入栈中即可，发现是右括号就要对比是否跟栈顶元素相匹配，不匹配就返回false

var isValid = function(s) {
    const map = { '{': '}', '(': ')', '[': ']' };
    const stack = [];
    for(let i of s){
        if(map[i]){
            stack.push(i);
        } else {
            if(map[stack[stack.length - 1]] === i){
                stack.pop()
            }else{
                return false;
            }
        }
    }
    return stack.length === 0;
};

155、 最小栈

先看题目：

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

• push(x) —— 将元素 x 推入栈中。
• pop() —— 删除栈顶的元素。
• top() —— 获取栈顶元素。
• getMin() —— 检索栈中的最小元素。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

pop、top 和 getMin 操作总是在 非空栈 上调用。

我们先不写getMin方法，满足其他方法实现就非常简单，我们来看一下：

var MinStack = function() {
    this.stack = [];
};

MinStack.prototype.push = function(x) {
    this.stack.push(x);
};

MinStack.prototype.pop = function() {
    this.stack.pop();
};

MinStack.prototype.top = function() {
    return this.stack[this.stack.length - 1];
};

如何保证每次取最小呢，我们举一个例子：

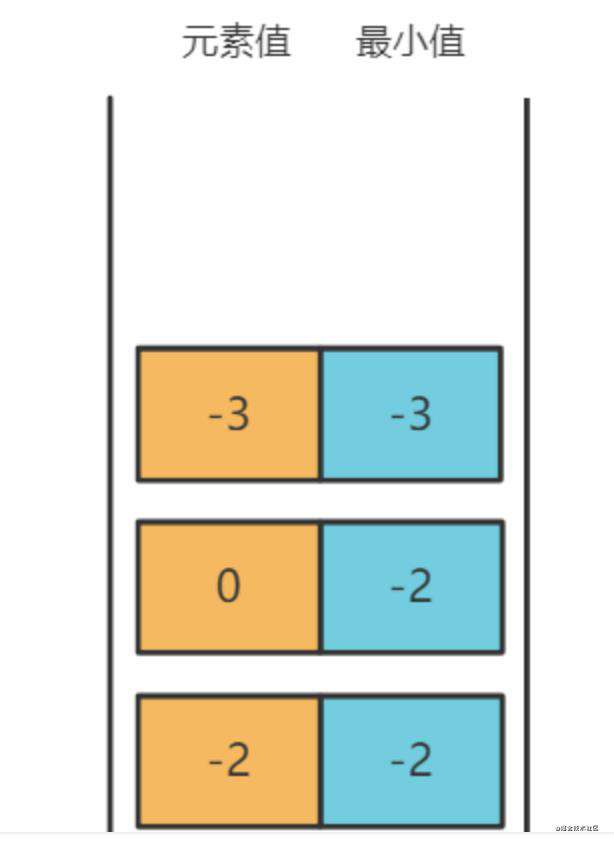
如上图，我们需要一个辅助栈来记录最小值，

• 开始我们向stack push -2
• 此时辅助栈minStack，因为此时stack最小的是-2，也push -2
• stack push 0
• 此时辅助站minStack 会用 0 跟 -2对比，-2更小，minstack会push -2
• stack push -3
• 此时辅助站minStack 会用 -3 跟 -2对比，-3更小，minstack会push -3

所以我们取最小的时候，总能在minStack中取到最小值，所以解法就出来了：

var MinStack = function() {
    this.stack = [];
    // 辅助栈
    this.minStack = [];
};

MinStack.prototype.push = function(x) {
    this.stack.push(x);
    // 如果是第一次或者当前x比最小栈里的最小值还小才push x
    if(this.minStack.length === 0 || x < this.minStack[this.minStack.length - 1]){
        this.minStack.push(x)
    } else {
         this.minStack.push( this.minStack[this.minStack.length - 1])
    }
};

MinStack.prototype.pop = function() {
    this.stack.pop();
    this.minStack.pop();
};

MinStack.prototype.top = function() {
    return this.stack[this.stack.length - 1];
};

MinStack.prototype.getMin = function() {
    return this.minStack[this.stack.length - 1];
};

动态规划

动态规划，一定要知道动态转移方程，有了这个，就相当于解题的钥匙，我们从题目中体会一下

53. 最大子序和

题目如下：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。  

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [0]
输出：0

思路：

• 这道题可以用动态规划来解决，关键是找动态转移方程
• 假设dp[i]：包括下标i之前的最大连续子序列和为dp[i]。

确定递推公式 dp[i]只有两个方向可以推出来：

• dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
• nums[i]，即：从头开始计算当前连续子序列和
• 一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

var maxSubArray = function(nums) {
  let res = nums[0];
  const dp = [nums[0]];
  for(let i=1;i < nums.length;i++){
      if(dp[i-1]>0){
        dp[i]=nums[i]+dp[i-1]
      }else{
       dp[i]=nums[i]
      }
      
    res=Math.max(dp[i],res)
  }
    return res
};

70. 爬楼梯

先看题目：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶
示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

涉及到动态规划，一定要知道动态转移方程，有了这个，就相当于解题的钥匙，

这道题我们假设dp[10]表示爬到是你爬到10阶就到达楼顶的方法数，

那么，dp[10] 是不是就是你爬到8阶，然后再走2步就到了，还有你走到9阶，再走1步就到了，

所以 dp[10] 是不是等于 dp[9]+dp[8]

延伸一下 dp[n] 是不是等于 dp[n - 1] + dp[n - 2]

代码如下：

var climbStairs = function(n) {
    const dp = {};
    dp[1] = 1;
    dp[2] = 2;
    for(let i = 3; i <= n; i++){
        dp[i] = dp[i-1] + dp[i-2]
    }
    return dp[n]
};

数学问题

以下更多的是涉及数学问题，这些解法非常重要，因为在中级题里面会经常用到，比如我们马上讲到的加一这个题， 中级的两数相加都是一个模板。

66. 加一

这个题的关键有两点：

• 需要有一个进位的变量carry记录到底进位是几
• 还需要一个每次迭代都重置和的变量sum来帮我们算是否进位，以及进位后的数字

var plusOne = function(digits) {
  let carry = 1; // 进位（因为我们确定+1，初始化进位就是1）
  for(let i = digits.length - 1; i >= 0; i--){
      let sum = 0; // 这个变量是用来每次循环计算进位和digits[i]的值的
      sum = digits[i] + carry; 
      digits[i] = sum % 10; // 模运算取个位数
      carry = (sum / 10) | 0; //  除以10是取百位数，并且｜0表示舍弃小数位
  }
  if(digits[0] === 0) digits.unshift(carry);
  return digits
};

69 x的平方根

题目如下： 实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2
示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

这道题是典型的二分法解题，所以我们需要熟悉二分法的通用模板，我们出一个题：

在 [1, 2, 3, 4, 5, 6, 7, 8, 9] 中找到 4，若存在则返回下标，不存在返回-1

funcion searchNum(target, nums){
     if(!nums.length) return -1;
     let l = 0;
     let r = nums[nums.length - 1];     
     while(l <= r){
         let mid = l + r >> 1
         if(nums[mid] === target) return mid;
         if(nums[mid] > target) {
             r--
         } else {
             l++
         }
     }
     return -1;
}

注意到题目中给出的例 2，小数部分将被舍去。我们就知道了，如果一个数 aa 的平方大于 xx ，那么 aa 一定不是 xx 的平方根。我们下一轮需要在 [0..a - 1][0..a−1] 区间里继续查找 xx 的平方根。

所以代码如下：

const mySqrt = x => {
    let [low, high] = [0, x];
    while (low <= high) {
        const mid = (low + high) >> 1;
        if (mid * mid > x) {
            high = mid - 1;
        } else if (mid * mid < x) {
            low = mid + 1;
        } else {
            return mid;
        }
    }
    return high;
};

171. Excel表序列号

这个题比较重要，也比较基础，简而言之就是进制转换

题目如下：

给你一个整数 columnNumber ，返回它在 Excel 表中相对应的列名称。

例如：

A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28 
...

示例 1：

输入：columnNumber = 1
输出："A"
示例 2：

输入：columnNumber = 28
输出："AB"
示例 3：

输入：columnNumber = 701
输出："ZY"
示例 4：

输入：columnNumber = 2147483647
输出："FXSHRXW"

说白了，这就是一道26进制的问题，以前我们知道10进制转2进制就是不停的除2，把余数加起来，26进制也是一样，不停的除26

思路：

• 从末尾开始取得每一个字符对应的数cur = c.charCodeAt() - 64
• 数字总和sum += 当前数 * 进制位数
• 进制位数 *= 26，初始化进制位数carry = 1

var titleToNumber = function(s) {
    let sum = 0, i = s.length - 1, carry = 1;

    while (i >= 0) {
        let cur = s[i].charCodeAt() - 64;

        sum += cur * carry;
        carry *= 26;
        i--;
    }

    return sum;
};

172. 阶乘中的零

题目： 给定一个整数 n，返回 n! 结果尾数中零的数量。

示例 1:

输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:

输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.

这道题很简单，有多少个5就有多少个0

var trailingZeroes = function (n) {
  let r = 0;
  while (n > 1) {
    n = parseInt(n / 5);
    r += n;
  }
  return r;
};

// ## 190.颠倒二进制位

268. 丢失的数字

题目如下：

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

进阶：

你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?  

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。
示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

这题很简单，就是用0-n的总和减去数组总和

• 0 - n 的总和用等差数列:（首数+尾数）* 项数 / 2 来求

 var missingNumber = function(nums) {
    const len = nums.length
 
   let sum = ((1 + len) * len) / 2
 
   for (let i = 0; i < len; i++) {
     sum -= nums[i]
   }
 
   return sum
 }

// - 3的幂

412. Fizz Buzz

这个题没啥好说的，就按照题目说的写代码就行，先看题目：

写一个程序，输出从 1 到 n 数字的字符串表示。

1. 如果 n 是3的倍数，输出“Fizz”；

2. 如果 n 是5的倍数，输出“Buzz”；

3. 如果 n 同时是3和5的倍数，输出 “FizzBuzz”。

示例：

n = 15,

返回:
[
    "1",
    "2",
    "Fizz",
    "4",
    "Buzz",
    "Fizz",
    "7",
    "8",
    "Fizz",
    "Buzz",
    "11",
    "Fizz",
    "13",
    "14",
    "FizzBuzz"
]

  var fizzBuzz = function (n) {
    const list = [];
    for (let i = 1; i <= n; i++) {
      const is3Times = i % 3 === 0; // 是否是3的倍数
      const is5Times = i % 5 === 0; // 是否是5的倍数
      const is15Times = is3Times && is5Times; // 是否是15的倍数
      if (is15Times) {
        list.push('FizzBuzz');
        continue;
      }
      if (is3Times) {
        list.push('Fizz');
        continue;
      }
      if (is5Times) {
        list.push('Buzz');
        continue;
      }
      list.push(`${i}`);
    }
    return list;
  };

• 7. 整数反转

稍后更新本文章

环问题

这类问题的特点就是，你要循环寻找，到底怎么循环寻找，看题便知。

141. 环形链表

题目如下：

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。 否则，返回 false 。

示例 1：

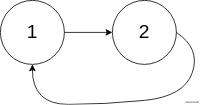
输入： head = [3,2,0,-4], pos = 1
输出： true
解释： 链表中有一个环，其尾部连接到第二个节点。

示例 2：

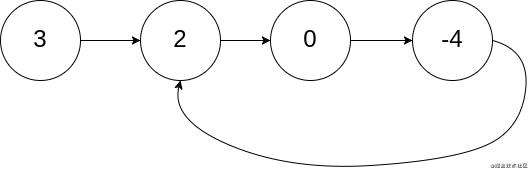
输入： head = [1,2], pos = 0
输出： true
解释： 链表中有一个环，其尾部连接到第一个节点。

我们采用标记法：

给遍历过的节点打记号，如果遍历过程中遇到有记号的说明已环

var hasCycle = function(head) {
    let traversingNode = head;
    while(traversingNode){
        if(traversingNode.isVistitd) return true
        traversingNode.isVistitd = true
        traversingNode = traversingNode.next
    }
    return false;
};

160. 相交链表

题目如下：

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

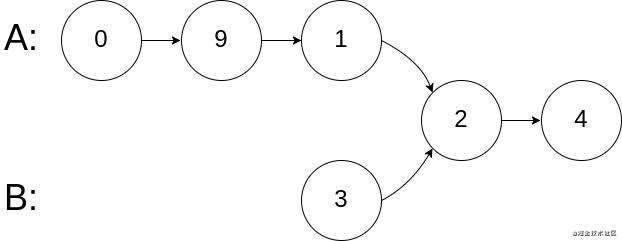
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

稍后更新本文章

202. 快乐数

题目如下： 编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果 可以变为  1，那么这个数就是快乐数。
• 如果 n 是快乐数就返回 true ；不是，则返回 false 。

快乐数怎么分析呢？

我们来看一个表，就会得出结论，一个数按照快乐数定义的方式分别每个数字平方，会有两种情况

• 1. 得到1
• 2. 无限循环

无限循环参照下图

有人会说会不会一直变大，答案是不会： 我们看下面列表，

• 可以看到如果你是13位，你的下一次快乐数算法会变为4位1053，
• 如果你是9999, 4位，下一个快乐数是324

所以代码只要判断这两种就行了，代码如下：

// 封装获取快乐数的方法
function getNext(n){
    n = String(n);
    let sum = 0;
    for(let num of n){
        sum = sum + Math.pow(+num, 2);
    }
    return sum;
}
var isHappy = function(n) {
    // 哈希表来看是否循环
    const map = {};
    while( n !== 1 ){
        map[n] = true;
        n = getNext(n)
        if(map[n]) return false
    }
    return true
};

后面会写中级算法的题，请大家务必把这些基础算法题掌握好，基础不牢地动山摇，后面中级题很多都是在这些基础题的基础上的。